In the previous chapter we looked at drawing in 3-dimensions using Processing’s P3D mode. Generating images of 3-dimensional scenes can be a process intensive job and even a moderately complex scene can quickly bring a highly specified PC to a crawl. The reason for this is simply that in P3D mode, the processing and drawing of 3-d scenes is handled entirely in software and this can tax even the most powerful CPUs. In contrast, most modern graphic cards implement 3-D drawing directly in hardware and can achieve speeds of an order of magnitude or more over pure software based solutions such as P3D. In this chapter we will see how Processing is able to offload drawing tasks to the graphics card of your PC and as a result render 2D and 3D sketches much faster.
There are two main frameworks to allow a program or application like Processing to harness the built in power of a graphics card. These are Microsoft D3D and OpenGL. D3D is owned by Microsoft and only supported on Windows. OpenGL on the other hand is cross platform and has broad support on the big three operating systems, Windows, Linux and Mac OS X. In addition, and crucially important for Processing, OpenGL is supported in Java though Sun’s JOGL library (JOGL is short for Java OpenGL). The following diagram shows a simplified view of Processing’s drawing stack.
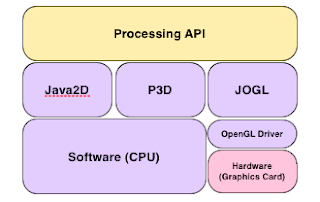
Processing provides a rich, uniform and simple API for drawing and rendering graphics,
but the actual drawing of pixels is performed by any one of the lower level libraries. Switching between libraries is easy, all you need to do is specify which one you would like to use in the third parameter of screen() (OpenGL also requires you import the Processing OpenGL library which interfaces Processing to JOGL). For example, to specify OpenGL you would include the following lines:
import processing.opengl.*;
void setup()
{
size( 1024, 768, OPENGL ) ;
}
From then on, the Processing runtime will use the JOGL library for all its underlying drawing operations and your sketch will benefit from any hardware acceleration your graphic card possesses.
OpenGL is not limited to sketches that use 3 dimensions, you can also use it for 2-d sketches. Try running sketches from other chapters in OpenGL mode and see how they behave. In practise sketches running in OpenGL mode will look somewhat different from the default JAVA2D mode. The changes may vary from no visual difference to quite dramatic changes. You may see an improvement in rendering quality and for graphic intensive sketches an increase in performance., However, if you are going to be sharing sketches with other people then you may prefer to stick with JAVA2D for 2D sketches. With JAVA2D you can be sure that your sketches will look consistent across different machines and that they will run regardless of whether OpenGL is installed or not.
In theory OpenGL mode should bring clear performance and rendering improvements to any sketch. The extent of these improvements however depends on your graphics card and the quality of the OpenGL drivers. In the first instance you need to make sure that OpenGL is installed for your machine. If you are using Mac OS X then congratulations, OpenGL will already be installed and you will more than likely have an OpenGL stress free experience. If you are using Linux or Windows you may first have to install the OpenGL drivers for your graphics card. If you are using a relatively new PC then this shouldn’t be too much of a traumatic experience, but if your graphics card is old or of an obscure make then finding the drivers may prove problematic. In addition, not all graphic cards are equal. Some will be faster, much faster than others, while others may not implement every feature of OpenGL. For example, early Macbooks use integrated graphics chip sets which do not support anti-aliasing. As a general rule of thumb though, discreet graphic cards are better at running OpenGL than integrated graphic chip sets.
Ball of Confusion
The example sketch for this chapter is Ball of Confusion. It uses a procedural technique to generate a 3D fractal ball. The program will generate thousands of triangles so it is a good test for OpenGL running on your machine. If you don’t have OpenGL installed then don’t worry, Ball of Confusion will also run in P3D mode. Just change the third parameter in setup() from OPENGL to P3D. Even if you have OpenGL installed and running, you may want to experiment with P3D to compare the difference in speed and rendering quality.
The term procedural means that the program will generating the scene geometry itself as opposed to drawing a 3D model designed by an artist. Procedural techniques are powerful and can generate some fascinating and amazingly beautiful images. Invariably they are rooted in mathematical methods, but don’t let that put you off – the concepts involved are usually very simple and yet can produce a wide range of imagery from complex, precise geometric objects to organic, flowing animations. In Ball of Confusion we will explore triangular subdivision to generate a fractal sphere using an icosahedron as a basis or seed. Processing has several built in primitive 3-d objects which you can plot very easily: for example, to plot a sphere you can use the sphere() function. The icosahedron however is not included and we will have to construct and draw the shape ourselves. If you’re not familiar with what an icosahedron looks like then fear not, Ball of Confusion will enlighten you!
The program is relatively short but it offers a rich playing field for experimentaion. So, at the end of this chapter I’ll discuss ways you can improve and extend Ball of Confusion, but for now lets make a start and look at the program in detail.
//
// BOC - v1
//
import processing.opengl.*;
void setup()
{
size( 1024, 768, OPENGL ) ;
colorMode( RGB, 1.0f ) ;
}
The setup() section looks much like any other sketch except for the use of OpenGL mode. OpenGL is specified by including the OpenGL library (the first line of the code) and then specifying OPENGL as the third parameter to screen(). These are the only changes you need to make to a sketch for it to run in OpenGL mode.
There is one other point to mention about setup() and that is the way I’ve set up the colour mode. You may be accustomed to using integer values in the range 0 - 255 for the colour components, but in BOC I’ve elected to use floating point values in the range 0 - 1.
The next part of BOC is the draw() function:-
void draw()
{
background( 0.25f ) ;
// Move the origin so that the scene is centered on the screen.
translate( width/2, height/2, 0.0f ) ;
// Set up the lighting.
ambientLight( 0.025f, 0.025f, 0.025f ) ;
directionalLight( 0.2f, 0.2f, 0.2f, -1, -1, -1);
spotLight( 1.0f, 1.0f, 1.0f, -200, 0, 300, 1, 0, -1, PI/4.0f, 20) ;
// Rotate the local coordiante system.
smoothRotation( 5.0f, 6.7f, 7.3f ) ;
// Draw the inner object.
noStroke() ;
fill( smoothColour( 10.0f, 12.0f, 7.0f ) ) ;
drawIcosahedron( 5, 60.0f, false ) ;
// Rotate the local coordiante system again.
smoothRotation( 4.5f, 3.7f, 7.3f ) ;
// Draw the outer object.
stroke( 0.2f ) ;
fill( smoothColour( 6.0f, 9.2f, 0.7f ) ) ;
drawIcosahedron( 5, 200.0f, true ) ;
}
We start of by clearing the screen. I’ve chosen a grey value of 0.25f which equates to the usual rgb value of (64,64,64). Next we translate the origin along the x and y axis so that the origin of our 3D scene will be projected to the centre of the screen. Without the call to translate() the scene would be drawn centred around the (not so terribly useful) default origin at the top left of the screen. We then set up some lights. We could have used the Processing function lights() to set up some default lighting, but instead I’ve opted for my own lights. The lighting I’ve chosen is dark and moody but this is easily changed.
Next we set up a rotating coordinate system that spins the scene around the origin in a smooth and cyclic fashion. To achieve this effect I’ve writen the utiltity function smoothVector(). I’ll explain how it works below but basically it sets up some rotations about the principal x and y axis. By the way, can you see why the call to translate() comes before the lights? Also, what would happen if you changed the order of the lights and rotation to this?
// Move the origin so that the scene is centered on the screen.
translate( width/2, height/2, 0.0f ) ;
// Rotate the local coordiante system.
smoothRotation( 5.0f, 6.7f, 7.3f ) ;
// Set up the lighting.
ambientLight( 0.025f, 0.025f, 0.025f ) ;
directionalLight( 0.2f, 0.2f, 0.2f, -1, -1, -1);
spotLight( 1.0f, 1.0f, 1.0f, -200, 0, 300, 1, 0, -1, PI/4.0f, 20) ;
Go ahead, try it out!
The remaining lines draw the two objects which make up the scene. For each object I set up the drawing style and colour first, and then draw the object as an icosahedron. The colours make use of another utility function smoothColour(), while the call to drawIcosahedron() takes three parameters, depth, radius and spherical. These three parameters determine the amount of detail in the icosahedron, its size and also its shape. If you haven’t run Ball of Confusion yet then now is probably a good time as the importance of these parameters will be apparent once you have seen BOC in action.
Lets take a look at smoothRotation() and smoothVector now.
/**
* Generate a vector whose components change smoothly over time in the range [ 0, 1 ].
* Each component uses a sin() function to map the current time in milliseconds somewhere
* in the range [ 0, 1 ].A 'speed' factor is specified for each component.
*/
PVector smoothVector( float s1, float s2, float s3 )
{
float mills = 0.00003f * millis() ;
float x = 0.5f * sin( mills * s1 ) + 0.5f ;
float y = 0.5f * sin( mills * s2 ) + 0.5f ;
float z = 0.5f * sin( mills * s3 ) + 0.5f ;
return new PVector( x, y, z ) ;
}
/**
* Generate a colour which smoothly changes over time.
* The speed of each component is controlled by the parameters s1, s2 and s3.
*/
color smoothColour( float s1, float s2, float s3 )
{
PVector v = smoothVector( s1, s2, s3 ) ;
return color( v.x, v.y, v.z ) ;
}
/**
* Rotate the current coordinate system.
* Uses smoothVector() to smoothy animate the rotation.
*/
void smoothRotation( float s1, float s2, float s3)
{
PVector r1 = smoothVector( s1, s2, s3 ) ;
rotateX( 2.0f * PI * r1.x ) ;
rotateY( 2.0f * PI * r1.y ) ;
rotateX( 2.0f * PI * r1.z ) ;
}
Both these functions animate a property over time. smoothColour() cycles through colours while smoothRotation() rotates the view in a progressive, cyclic fashion. To give these changes an element of unpredictability, the functions take parameters s1, s2, and s3. The value of these parameters determine how fast each component changes. So for example in smoothColour() s1, s2 and s3 determine how fast the red, green and blue channels change relative to each other.
Although these methods animate entirely different properties they are very similar in functionality. So much so in fact that I’ve broken out the common code as the separate function smoothVector(). This function takes the three parameters, s1, s2 and s3, and returns as a vector the three component values animated in the range [ 0, 1] (a vector is a triplet of numbers and Processing provides us with PVector, an extremely useful class for manipulating vectors directly).
To achieve a smooth and cyclic rhythm smoothValue() uses the sine function with the current time in milliseconds (multiplied by s1, s2 or s3) as the argument. The return value is a PVector and the x, y and z properties of this vector are used for the components of the rotation and colour.
The next section of code calculates the verticies of the icosahedron (an icosahedron is one of the five Platonic solids and consists of 20 identical triangular faces), and then proceeds to draw it. Don’t worry if the code looks complicated because it is in fact quite straight forward if not a bit monotonous. The details aren’t that important but if geometry is your thing you might find the method of construction interesting and useful for other projects.
/**
* Draw an icosahedron defined by a radius r and recursive depth d.
* Geometry data will be saved into dst. If spherical is true then the icosahedron
* is projected onto the sphere with radius r.
*/
void drawIcosahedron( int depth, float r, boolean spherical )
{
// Calcualte the vertex data for an icosaheron inscribed by a sphere radius 'r'.
// Use 4 Golden Ratio rectangles as the basis.
float gr = ( 1.0f + sqrt(5.0f) ) / 2.0f ;
float h = r / sqrt( 1.0f + gr * gr ) ;
PVector[] v =
{
new PVector( 0,-h,h*gr ), new PVector( 0,-h,-h*gr ), new PVector( 0,h,-h*gr ), new PVector( 0,h,h*gr ),
new PVector( h,-h*gr,0 ), new PVector( h,h*gr,0 ), new PVector( -h,h*gr,0 ), new PVector( -h,-h*gr,0 ),
new PVector( -h*gr,0,h ), new PVector( -h*gr,0,-h ), new PVector( h*gr,0,-h ), new PVector( h*gr,0,h )
} ;
// Draw the 20 triangular faces of the icosahedron.
if ( ! spherical )
r = 0.0f ;
beginShape( TRIANGLES ) ;
drawTriangle( depth, r, v[0], v[7],v[4] ) ;
drawTriangle( depth, r, v[0], v[4], v[11] ) ;
drawTriangle( depth, r, v[0], v[11], v[3] ) ;
drawTriangle( depth, r, v[0], v[3], v[8] ) ;
drawTriangle( depth, r, v[0], v[8], v[7] ) ;
drawTriangle( depth, r, v[1], v[4], v[7] ) ;
drawTriangle( depth, r, v[1], v[10], v[4] ) ;
drawTriangle( depth, r, v[10], v[11], v[4] ) ;
drawTriangle( depth, r, v[11], v[5], v[10] ) ;
drawTriangle( depth, r, v[5], v[3], v[11] ) ;
drawTriangle( depth, r, v[3], v[6], v[5] ) ;
drawTriangle( depth, r, v[6], v[8], v[3] ) ;
drawTriangle( depth, r, v[8], v[9], v[6] ) ;
drawTriangle( depth, r, v[9], v[7], v[8] ) ;
drawTriangle( depth, r, v[7], v[1], v[9] ) ;
drawTriangle( depth, r, v[2], v[1], v[9] ) ;
drawTriangle( depth, r, v[2], v[10], v[1] ) ;
drawTriangle( depth, r, v[2], v[5], v[10] ) ;
drawTriangle( depth, r, v[2], v[6], v[5] ) ;
drawTriangle( depth, r, v[2], v[9], v[6] ) ;
endShape() ;
}
The first few lines use three orthogonal Golden Ratio rectangles inscribed by a sphere of radius ‘r’ to calculate the coordinates of the twelve verticies of the icosahedron. The remaining lines draw the 20 triangular faces made from the twelve verticies. The twist in this section of code is that the drawing of the triangles is deferred to a separate method. In doing so, we open up the possibility of manipulating the triangles before actually drawing them.
drawTriangle() is the most interesting part of the program so let’s examine it in detail and see how it implements the subdivision technique that is characteristic of Ball of Confusion.
/**
* Draw a triangle either immediately or subdivide it first.
* If depth is 1 then draw the triangle otherwise subdivide first.
*/
void drawTriangle( int depth, float r, PVector p1, PVector p2, PVector p3 )
{
if ( depth == 1 )
{
vertex( p1.x, p1.y, p1.z ) ;
vertex( p2.x, p2.y, p2.z ) ;
vertex( p3.x, p3.y, p3.z ) ;
}
else
{
// Calculate the mid points of this triangle.
PVector v1 = PVector.mult( PVector.add( p1, p2 ), 0.5f ) ;
PVector v2 = PVector.mult( PVector.add( p2, p3 ), 0.5f ) ;
PVector v3 = PVector.mult( PVector.add( p3, p1 ), 0.5f ) ;
if ( r != 0.0f )
{
// Project the verticies out onto the sphere with radius r.
v1.normalize() ; v1.mult( r ) ;
v2.normalize() ; v2.mult( r ) ;
v3.normalize() ; v3.mult( r ) ;
}
// Generate the next level of detail.
depth -- ;
drawTriangle( depth, r, p1, v1, v3 ) ;
drawTriangle( depth, r, v1, p2, v2 ) ;
drawTriangle( depth, r, v2, p3, v3 ) ;
// Uncomment out the next line to include the central part of the triangle.
// drawTriangle( depth, r, v1, v2, v3 ) ;
}
}
The function takes five parameters, a depth, a radius r and the coordinates of the triangle’s three verticies. If the value of the depth parameter is equal to one the triangle is drawn immediately. If however the depth value is not one, the triangle is subdivided into four smaller triangles. These smaller triangles are then processed using drawTriangle() but this time with a depth value one less. The process of subdivision repeats until the depth value reaches one and which point the resulting sequence of triangles is drawn. The diagram below shows this process in action for an initial triangle of depth 3.
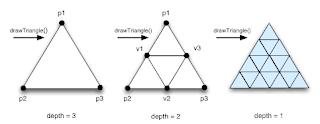

To perform the subdivision we need to calculate the point midway along an edge of a triangle. This is accomplished by taking the average of the two verticies that define the edge. To take the average of two numbers we just add them and divide by two. For example, the average of 3 and 9 is (3+9)/2=6. The same calcualtion is used for verticies, for example the average of the verticies (3,6,9) and (9,4,5) is (6,5,7). We can simplify the coding of this calculation by making use of the PVector class once again.
PVector v1 = PVector.mult( PVector.add( p1, p2 ), 0.5f ) ;
Here we store and manipulate the verticies of the triangle as PVectors, PVector.add() adds the components of two vectors to produce another vector and PVector.mult() scales a vector by a value.
The function drawTriangle() is an example of a recursive method and it is this property that gives Ball of Confusion the procedural quality I mentioned earlier. The fractal appearance of the objects comes from the fact that the code doesn’t actually draw the central triangle of each subdivision (that line has been commented out). So, at each level of detail, there is a triangle missing. To see this effect in greater detail try drawing the outer object with a depth value of 6.
// Draw the outer object.
stroke( 0.2f ) ;
fill( smoothColour( 6.0f, 9.2f, 0.7f ) ) ;
drawIcosahedron( 5, 200.0f, true ) ;
You could try even higher values but each increase in depth results in three times as many triangles drawn! Also with each increase in depth, the triangles decrease in area by a factor of four so detail will be lost when triangles approach the size of a single screen pixel.
There is one last feature of drawTriangle() to explain. You may be wondering how Ball of Confusion actually manages to draw a sphere from an icosahedron. Well, the radius parameter ‘r’ controls this action. The second if statement checks the value of r. If r equals 0 then the triangle is drawn without modifying the verticies and the icosahedron is drawn as an icosahedron. If r is not equal to 0 then the verticies of the triangle are projected out onto the surface of the sphere with radius r. You can imagine this action as blowing up the icosahedron like a balloon until it is squashed up against a surrounding sphere. To achieve this effect the PVector class is used once again to perform some mathematical trickery,
v1.normalize() ; v1.mult( r ) ;
v2.normalize() ; v2.mult( r ) ;
v3.normalize() ; v3.mult( r ) ;
The call to normalize() performs the projection to a sphere of radius 1. The mult() then scales the vertex to a sphere of radius r.
And that brings us to the end of the code!
To end this chapter I would like to suggest a few ways of improving and extending Ball of Confusion. From an artistic point of view you could try altering and adding lights, or even animate them in position and colour; Experiment with subdividing the 4 other Platonic solids; Try changing the colour of the triangles based on the current depth or triangle index. The geometric perfection of Ball of Confusion can be broken by adding some randomness to the size and position of the triangles, perhaps linked to the vertex depth. From a programming point of view, performance can be improved by calculating the geometry once and drawing the triangles from an array, thus avoiding the expensive recursive call on every animation frame.
I hope you have have success running Ball of Confusion in OpenGL mode. If not don’t forget you can always try it in P3D mode!








